Geometric Audio 3: Gauss Circle Problem for Integer Sized Room Models (part 2)

Recall in the previous post our derivation of the Gauss circle recurrence relation generalized to arbitrary dimensions, scaling, offset, and weights:

s_weighting

where the cost of computing for $q: 0 \leq q \leq K^2$ for max-distance $K$ requires $O(D K^3)$ flops. In practice, the summation should be transposed so that $q$ is incremented within the inner loop as to take advantage of vectorization/SIMD memory access patterns.

A second approach for those familiar with DSP utilizes the fact that the summation term in the recurrence relation passes as a form of sparse convolution due to the quadratic-striding memory access patterns of $\hat{S}(q-(\Delta_D + \ell_D i), D-1))$ . To make the convolution operation explicit, we can vectorize $w_D^{|i|}$ into a sparse signal $f(m,D)$ and re-express the summation as follows:

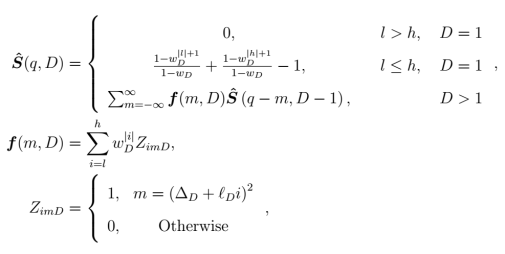
where $Z$ is an indicator variable. Note that in consideration of building $f(m,D)$ , a larger boundary scaling term $\ell_D$ increases the signal sparsity. i.e. from a computational perspective, there are regions in the parameter space of $(\ell_D, K)$ where either direct sparse-convolution or the direct evaluation of the recurrence relation will be faster than an implementation dependent Fast Fourier Transform (FFT) based convolution despite the latter’s lower asymptotic cost of $O(D K^2 \log(K))$ flops.

With the $L_2$ distance bound and Gauss circle problem out of the way, we will continue our investigation of lattice volume bounds in terms of the $L_1$ or taxi-cab distance in the next post.

4 thoughts on “Geometric Audio 3: Gauss Circle Problem for Integer Sized Room Models (part 2)”

[…] The cost of directly computing at is given by flops. Summing over all gives a cost of flops and is most expensive when the boundary size is minimized. This is certainly a large improvement over directly processing individual image-sources where the asymptotic costs of the two methods match for . However, we can make one last improvement by observing that the access patterns of resembles that of the convolution operation, allowing us to achieve even lower asymptotic cost of via the fast Fourier transform. Implementation details will be covered in the next post! […]

LikeLike

[…] produces a density estimation which forgoes processing individual image-sources. See part 1 and part 2. Related: Gauss Circle problem, dynamic programming, and Fourier […]

LikeLike

[…] direct computation in these spaces is expensive but some clever maths [see tutorial (parts 1, 2, 3, 4)] reduced the asymptotic costs to the point of practical use (e.g. a Reverb plugin). […]

LikeLike