Geometric Audio 4: Taxi-Cab Distance Bounds on Integer Lattice Maps

Recall from the introductory post, the taxi-cab distance metric on the integer lattice map relates the max-order of image-sources to the lattice volume or the total number of image-sources contained within a $k$ radius $L_1$ “ball”. This quantity is useful for determining the total costs of processing individual image-sources in cases where $k$ can be known or estimated beforehand (e.g. $k$ selected according to an estimate of a room’s RT60 using Sabine’s Equation).

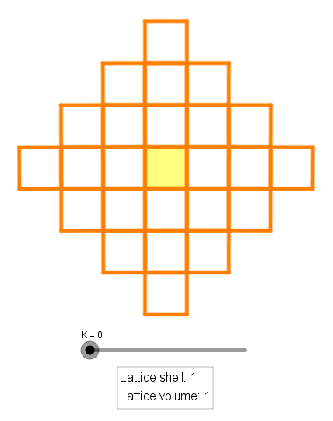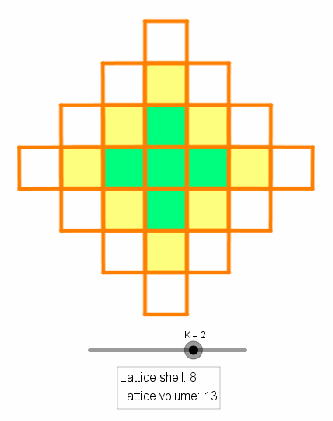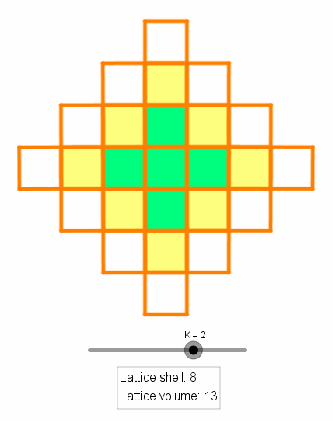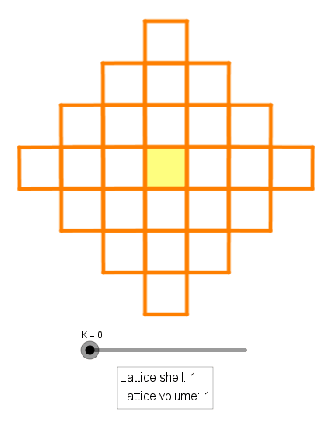
In $D$ dimensional space, the $L_1$ norm is given by $||\nu||_1 = \sum_{d=1}^D |\nu_d|$ where the lattice volume is defined by the number of integer lattice coordinates $||\nu||_1 \leq k$ . The visual equal-distance curve resembles a diamond in $D=2$ and the growth rate of the lattice volume seems obvious if we introduce a lattice-shell term given by the number of integer coordinates that satisfies $||\nu||_1 = k$ (see the animation below). Such ease is not the case for dimensions $D>2$ .

Lattice shell adds to growth of the lattice volume with respect to image-source order $k$

We start with a counting argument that relates the lattice shell and lattice volumes across dimensions via a recurrence relation:

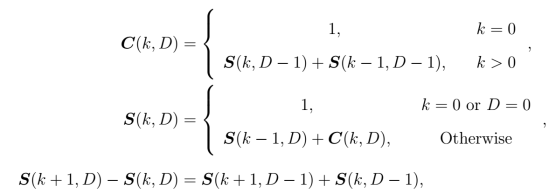
The lattice shell relation $C(k,D)$ follows from observation that all lattice coordinates on the boundary can be formed by augmenting $||\hat{\nu} ||_1 \leq k, \hat{\nu} \in Z^{D-1}$ with $\tilde{\nu}_D = k-||\hat{\nu}||_1$ and $||\tilde{\nu} ||_1 \leq k-1, \tilde{\nu} \in Z^{D-1}$ with $\tilde{\nu}_D = -(k-||\tilde{\nu}||_1)$ . The lattice volume relation $S(k,D)$ follows from the definition of a lattice shell which through substitution can be re-written as self-referential difference equation between successive dimensions. The counting solution is practical for small $k$ and $D$ but can be improved by the following ansatz.

Ansatz: Suppose that the lattice volume can be expressed as a polynomial equation given by $S(k, D) = 1 + \sum_{d=1}^D P_{d,D} k^d$ . Substitution into the difference equation gives

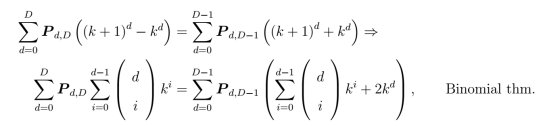
where $P_{d,D}$ are unknown polynomial coefficients of the powers of radius $k$ . Using the binomial theorem, the powers of $k$ rearranged as to form a generalized square matrix-system given by

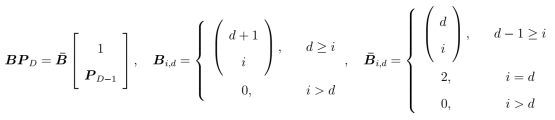
where upper triangular matrices $B, \bar{B}$ contain the binomial coefficients and $P_D$ is the vector of unknown polynomial coefficients to be solved for in terms of the polynomial coefficients $P_{D-1}$ in the preceding dimension. Carrying the recursion out from the base case $S(k, D=1) = 1+2k$ , the higher-dimensional lattice volumes are given by

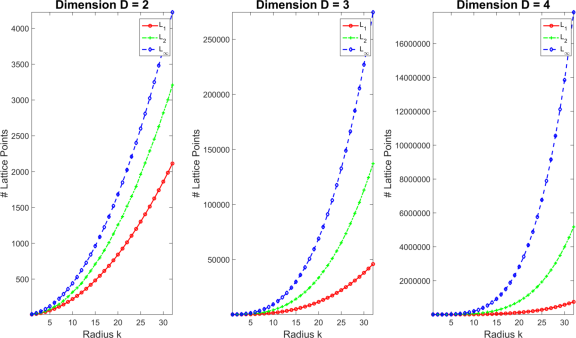
where by inspection, the highest order coefficients decrease towards $0$ as $D$ increases. This is expected as the majority of the volume moves towards the origin as $D$ grows. For some context, we can compare the lattice volumes bounded under larger p-norms such as $L_2$ or Euclidean (see post on Gauss circle problem, volume appx. hypersphere) and the $L_{\infty}$ norm given by $||\nu||_{\infty} = \max \{ |\nu_1|, \hdots, |\nu_D|\}$ (lattice volume trivially $(2k+1)^D$ ). By inspection, the lattice volume gap between $L_1$ and $L_2$ grows wider as the leading polynomial terms of $L_1$ decay to $0$ (see plot below).

This concludes our four-part foray into image-source models within high-dimensional integer lattice maps. If any new or interesting results come up or any errors found, I will update accordingly.

Notes: Animations generated in GeoGebra, equations and figures were from my draft paper.

3 thoughts on “Geometric Audio 4: Taxi-Cab Distance Bounds on Integer Lattice Maps”

Geometric Audio 1: Image-Source Room Models – NuSpace Audio

February 15, 2017 at 11:01 pm Reply

[…] to process individual image-sources within DSP pipelines (e.g. updating a tapped delay-line). See post. Related: linear algebra and dynamic […]

LikeLike
Geometric Audio 3: Gauss Circle Problem for Integer Sized Room Models (part 2) – NuSpace Audio

February 21, 2017 at 8:15 pm Reply

[…] With the distance bound and Gauss circle problem out of the way, we will continue our investigation of lattice volume bounds in terms of the or taxi-cab distance in the next post. […]

LikeLike
Riviera: Fast hybrid reverb plugin for modeling high-dimensional spaces – NuSpace Audio

October 15, 2017 at 7:51 am Reply

[…] direct computation in these spaces is expensive but some clever maths [see tutorial (parts 1, 2, 3, 4)] reduced the asymptotic costs to the point of practical use (e.g. a Reverb plugin). Parameterizing […]

LikeLike