Geometric Audio 2: Gauss Circle Problem for Integer Sized Room Models

In the previous post on image-sources for room modeling, we made the observations that

There exist a unique path from each image-source coordinate that can be back-traced to a receiver
The distance and direction between image-source coordinate and listener are equal sum total of the back-traced ray lengths and the final leg of the back-traced path respectively.
Image-source coordinates in 2D orthotopes has one-to-one mapping to integer lattice points
The number of image-sources with respect to reflection order $K$ and dimension $D$ is $O(K^D)$

For large $K$ or large $D$ , the number of image-sources becomes too large to process individually for any practical real-time applications. Instead, we ought to take a density estimation approach by making the following query: How many image-sources lie between a hypersphere of radius $k_1$ and $k_2$ centered about a receiver $L$ ? i.e. what is the difference in “lattice volume” or number of lattice points contained between two hyperspheres of different radii? If we can quickly solve for such queries, then it should be possible to design a multi-tap finite impulse response (FIR) where each sample is a weighted function of the differences in lattice volumes at successive radius $k=t \frac{v}{Fs}$ in meters ( $v$ is the velocity of sound, $Fs$ is the sample-rate, and $t$ is the integer sample index). To attack this problem, let us consider the classic Gauss Circle Problem posed simply as the determination of the number of integer lattice points within a circle of radius $k$ (see animation below).

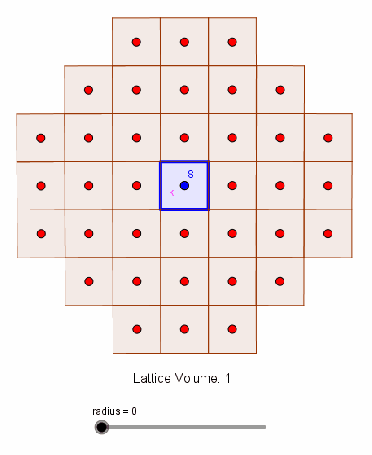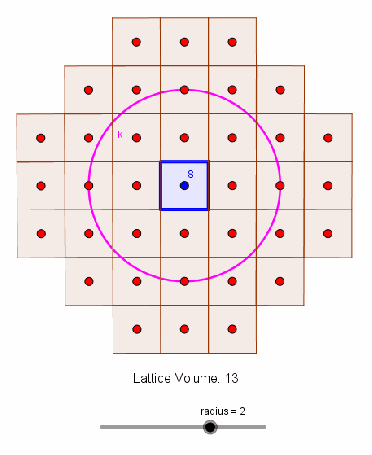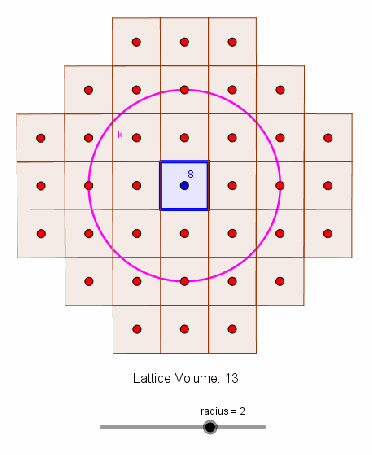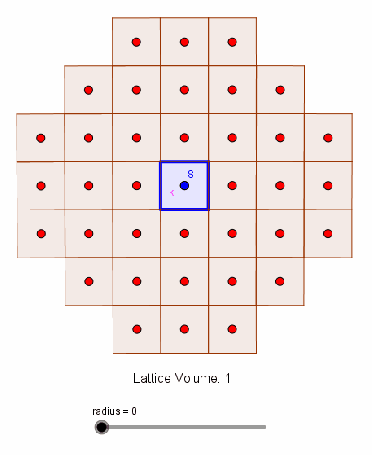
Gauss Circle.gif — 2D Gauss circle problem

The exact solution is known and given by $S(k) = 1+4\left \lfloor k \right \rfloor + 4\sum_{i=1}^{\left \lfloor k \right \rfloor} \left \lfloor \sqrt{k^2 - i^2} \right \rfloor$ , requiring an expensive summation over the positive integers less than $k$ . i.e. we must numerically count despite the fact that the lattice volume approaches the area of a circle as $k$ grows large if we want to model high-frequencies in our FIR.

Unfortunately, mapping our image-source density problem to the Gauss circle problem introduces many unsatisfactory constraints:

Number of dimensions restricted to $D = 2$
The room must be a unit square
Emitter and receiver are coincident to the origin
Each lattice point contributes only one unit to the summation (they are unweighted)
Area is a quadratic function of $k$ so later summations will be huge

Let us generalize the Gauss circle problem so that these constraints can be either removed or relaxed. For reference, Euclidean or $L_2$ distance in $D$ dimensions is given by

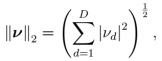
Recurrence relation for lattice volume $S(k,D)$ in arbitrary dimensions:

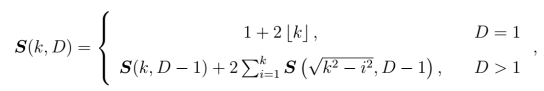
The base case for $D=1$ assumes that positive and negative lattice points coordinates are symmetric. For higher dimensional cases, we do a form of recursive integration over the positive integers of each dimension (see animation below).

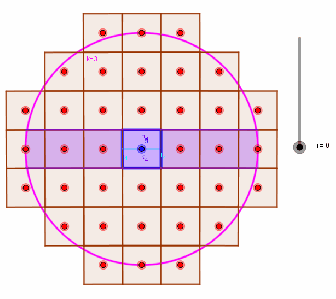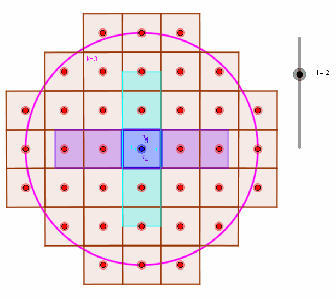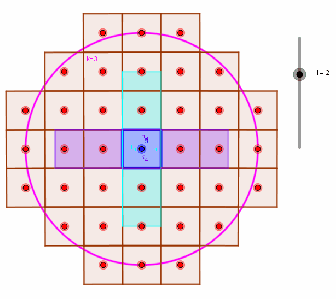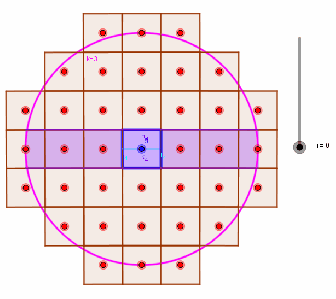
Purple region represents lattice volume at $\sqrt{k^2 - i^2}$ in $D=1$ as $i$ increases in $D=2$ .

This proof follows from the observation that if $||\nu||_2 \in \mathcal{R}^D \leq k$ and $\nu_D = i$ , then $\sum_{d=1}^{D-1} \nu_d^2 \leq k^2 - i^2$ .
Memorization in quadratic space:

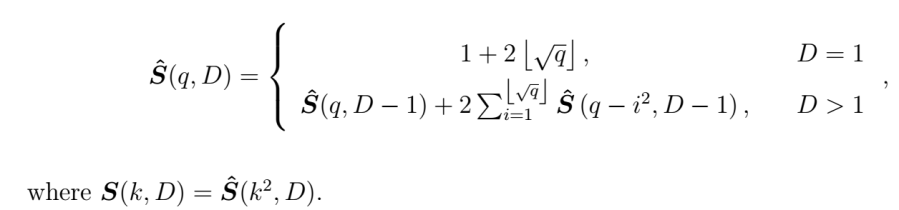
Lower dimensional solutions of the original recursive formulation can be stored in memory by mapping integer space $k$ to the quadratic space $k^2$ . i.e. We compute and store $\hat{S}(q, D)$ for $0 \leq q \leq K^2$ where $K$ is the max radius of interest (in practical terms, $K$ is a meter distance quantity converted from a desired reverb time). The trade-off is that memory requirements undergo quadratic scaling with respect to max radius.
Integer scaling of room boundaries and receiver offset:

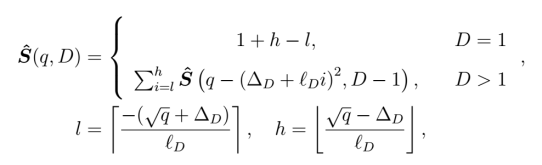
where integer scalar $\ell_D$ determines the size of room along dimension $D$ and integer scalar $\Delta_D: 0 \leq \Delta_D \leq \left \lfloor \frac{\ell_D}{2} \right \rfloor$ is the emitter offset in dimension $D$ from the origin. The proof follows from the constraint that $q - (\Delta_D + \ell_D i)^2 \geq 0$ implies $\sqrt{q} \geq \Delta_D + \ell_D i$ and $-\sqrt{q} \leq \Delta_D + \ell_D i$ .
Exponential decaying lattice point contributions:

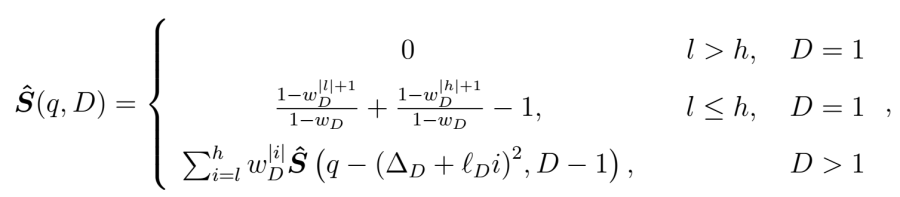
where $w_D: 0 \leq w_D \leq 1$ is a real value representing in physical terms a conversion of dB loss to magnitude due to a reflection off a boundary. Proof of the case of $l \leq h, D=1$ follows the application of the geometric series.

With the generalization of the Gauss circle problem into a dynamic programming problem, we have expanded the parameter space to include arbitrary dimensional orthotopes of integer boundary sizes, integer receiver offsets, and real reflection gain/loss coefficients. Prefiguring these parameters beforehand and accounting for attenuation loss due to a generalization of the inverse square law of sound-fields into higher dimensions, an RT60 or FIR length and subsequent max meters $K$ terms can be specified beforehand.

The cost of directly computing $\hat{S}(q, D)$ at $q$ is given by $O(\sqrt{q}/\ell_D)$ flops. Summing over all $0 \leq q \leq K^2$ gives a cost of $O(D K^3)$ flops and is most expensive when the boundary size $\ell_D =1$ is minimized. This is certainly a large improvement over directly processing $O(K^D)$ individual image-sources where the asymptotic costs of the two methods match for $D=3$ . However, we can make one last improvement by observing that the access patterns of $q, i \in \hat{S}(q - (\Delta_D + \ell_D i)^2, D-1)$ resembles that of the convolution operation, allowing us to achieve even lower asymptotic cost of $O(D K^2 \log K)$ via the fast Fourier transform. Implementation details will be covered in the next post!

———-

Notes: Equations were lifted from a draft paper that I’m writing. Animations were done with GeoGebra.

4 thoughts on “Geometric Audio 2: Gauss Circle Problem for Integer Sized Room Models”

Geometric Audio 3: Gauss Circle Problem for Integer Sized Room Models (part 2) – NuSpace Audio

February 14, 2017 at 11:27 pm Reply

[…] in the previous post our derivation of the Gauss circle recurrence relation generalized to arbitrary […]

LikeLike
Geometric Audio 1: Image-Source Room Models – NuSpace Audio

February 15, 2017 at 1:41 pm Reply

[…] produces a density estimation which forgoes processing individual image-sources. See post. Related: Gauss Circle problem, dynamic programming, and Fourier […]

LikeLike
Geometric Audio 4: Taxi-Cab Distance Bounds on Integer Lattice Maps – NuSpace Audio

February 15, 2017 at 10:37 pm Reply

[…] we can compare the lattice volumes bounded under larger p-norms such as or Euclidean (see post on Gauss circle problem, volume appx. hypersphere) and the norm given by (lattice volume […]

LikeLike
Riviera: Fast hybrid reverb plugin for modeling high-dimensional spaces – NuSpace Audio

October 15, 2017 at 7:51 am Reply

[…] direct computation in these spaces is expensive but some clever maths [see tutorial (parts 1, 2, 3, 4)] reduced the asymptotic costs to the point of practical use (e.g. a Reverb plugin). […]

LikeLike