In the previous post on image-sources for room modeling, we made the observations that
- There exist a unique path from each image-source coordinate that can be back-traced to a receiver
- The distance and direction between image-source coordinate and listener are equal sum total of the back-traced ray lengths and the final leg of the back-traced path respectively.
- Image-source coordinates in 2D orthotopes has one-to-one mapping to integer lattice points
- The number of image-sources with respect to reflection order
and dimension
is
For large or large
, the number of image-sources becomes too large to process individually for any practical real-time applications. Instead, we ought to take a density estimation approach by making the following query: How many image-sources lie between a hypersphere of radius
and
centered about a receiver
? i.e. what is the difference in “lattice volume” or number of lattice points contained between two hyperspheres of different radii? If we can quickly solve for such queries, then it should be possible to design a multi-tap finite impulse response (FIR) where each sample is a weighted function of the differences in lattice volumes at successive radius
in meters (
is the velocity of sound,
is the sample-rate, and
is the integer sample index). To attack this problem, let us consider the classic Gauss Circle Problem posed simply as the determination of the number of integer lattice points within a circle of radius
(see animation below).

The exact solution is known and given by , requiring an expensive summation over the positive integers less than
. i.e. we must numerically count despite the fact that the lattice volume approaches the area of a circle as
grows large if we want to model high-frequencies in our FIR.
Unfortunately, mapping our image-source density problem to the Gauss circle problem introduces many unsatisfactory constraints:
- Number of dimensions restricted to
- The room must be a unit square
- Emitter and receiver are coincident to the origin
- Each lattice point contributes only one unit to the summation (they are unweighted)
- Area is a quadratic function of
so later summations will be huge
Let us generalize the Gauss circle problem so that these constraints can be either removed or relaxed. For reference, Euclidean or distance in
dimensions is given by

- Recurrence relation for lattice volume
in arbitrary dimensions:

The base case forassumes that positive and negative lattice points coordinates are symmetric. For higher dimensional cases, we do a form of recursive integration over the positive integers of each dimension (see animation below).

Purple region represents lattice volume at in
as
increases in
.
This proof follows from the observation that if
and
, then
.
- Memorization in quadratic space:
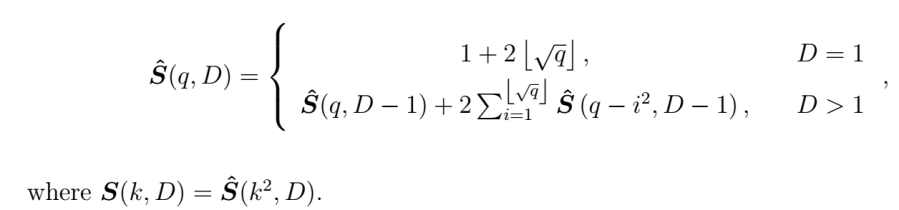
Lower dimensional solutions of the original recursive formulation can be stored in memory by mapping integer spaceto the quadratic space
. i.e. We compute and store
for
where
is the max radius of interest (in practical terms,
is a meter distance quantity converted from a desired reverb time). The trade-off is that memory requirements undergo quadratic scaling with respect to max radius.
- Integer scaling of room boundaries and receiver offset:

where integer scalardetermines the size of room along dimension
and integer scalar
is the emitter offset in dimension
from the origin. The proof follows from the constraint that
implies
and
.
- Exponential decaying lattice point contributions:
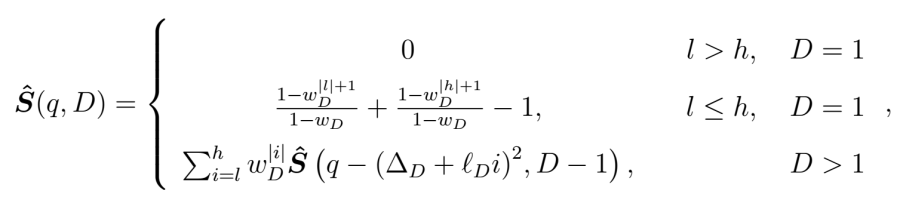
whereis a real value representing in physical terms a conversion of dB loss to magnitude due to a reflection off a boundary. Proof of the case of
follows the application of the geometric series.
With the generalization of the Gauss circle problem into a dynamic programming problem, we have expanded the parameter space to include arbitrary dimensional orthotopes of integer boundary sizes, integer receiver offsets, and real reflection gain/loss coefficients. Prefiguring these parameters beforehand and accounting for attenuation loss due to a generalization of the inverse square law of sound-fields into higher dimensions, an RT60 or FIR length and subsequent max meters terms can be specified beforehand.
The cost of directly computing at
is given by
flops. Summing over all
gives a cost of
flops and is most expensive when the boundary size
is minimized. This is certainly a large improvement over directly processing
individual image-sources where the asymptotic costs of the two methods match for
. However, we can make one last improvement by observing that the access patterns of
resembles that of the convolution operation, allowing us to achieve even lower asymptotic cost of
via the fast Fourier transform. Implementation details will be covered in the next post!
———-
Notes: Equations were lifted from a draft paper that I’m writing. Animations were done with GeoGebra.

[…] in the previous post our derivation of the Gauss circle recurrence relation generalized to arbitrary […]
LikeLike
[…] produces a density estimation which forgoes processing individual image-sources. See post. Related: Gauss Circle problem, dynamic programming, and Fourier […]
LikeLike
[…] we can compare the lattice volumes bounded under larger p-norms such as or Euclidean (see post on Gauss circle problem, volume appx. hypersphere) and the norm given by (lattice volume […]
LikeLike
[…] direct computation in these spaces is expensive but some clever maths [see tutorial (parts 1, 2, 3, 4)] reduced the asymptotic costs to the point of practical use (e.g. a Reverb plugin). […]
LikeLike